9.25三角形最小路径和

题目：

1
2
3
给定一个三角形 triangle ，找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

示例:

1
2
3
4
5
6
7
8
输入：triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出：11
解释：如下面简图所示：
   2
  3 4
 6 5 7
4 1 8 3
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

答案：

解法一：自上而下动态规划带备忘录：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int minimumTotal(int** triangle, int triangleSize, int* triangleColSize) {
    int f[triangleSize][triangleSize];
    memset(f,0,sizeof(f));
    f[0][0] = triangle[0][0];
    for (int i = 1; i < triangleSize; ++i) {
        f[i][0] = f[i - 1][0] + triangle[i][0];
        for(int j = 1; j < i; ++j) {
            f[i][j] = fmin(f[i - 1][j - 1],f[i - 1][j]) + triangle[i][j];
        }
        f[i][i] = f[i - 1][i - 1] + triangle[i][i];
    }
    int ret = f[triangleSize - 1][0];
    for(int i = 1; i < triangleSize; i++)
        ret = fmin(ret,f[triangleSize - 1][i]);
    return ret;
}

解法二:根据奇偶划分优化存储：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int minimumTotal(int** triangle, int triangleSize, int* triangleColSize) {
    int f[2][triangleSize];
    memset(f, 0, sizeof(f));
    f[0][0] = triangle[0][0];
    for (int i = 1; i < triangleSize; ++i) {
        int curr = i % 2;
        int prev = 1 - curr;
        f[curr][0] = f[prev][0] + triangle[i][0];
        for (int j = 1; j < i; ++j) {
            f[curr][j] = fmin(f[prev][j - 1], f[prev][j]) + triangle[i][j];
        }
        f[curr][i] = f[prev][i - 1] + triangle[i][i];
    }
    int ret = f[(triangleSize - 1) % 2][0];
    for (int i = 1; i < triangleSize; i++)
        ret = fmin(ret, f[(triangleSize - 1) % 2][i]);
    return ret;
}

9.26有效三角形个数

题目：

1
给定一个包含非负整数的数组 nums ，返回其中可以组成三角形三条边的三元组个数。

示例:

1
2
3
4
5
6
输入: nums = [2,2,3,4]
输出: 3
解释:有效的组合是: 
2,3,4 (使用第一个 2)
2,3,4 (使用第二个 2)
2,2,3

答案：

解法一，排序+二分查找:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int cmp(const void* a, const void* b) {
    return (*(int*)a - *(int*)b);
}
int triangleNumber(int* nums, int numsSize) {
    qsort(nums, numsSize,sizeof(int),*cmp);
    int ans = 0;
    for(int i = 0; i < numsSize; ++i) {
        for(int j = i + 1; j < numsSize; ++j) {
            int left = j + 1, right = numsSize - 1, k = j;
            while(left <= right) {
                int mid = (left + right) / 2;
                if(nums[mid] < nums[i] + nums[j]) {
                    k = mid;
                    left = mid + 1;
                }else {
                    right = mid - 1;
                }
            }
            ans += k-j;
        }
    }
    return ans;
}

优化后，解法二：双指针:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int cmp(const void* a, const void* b) {
    return (*(int*)a - *(int*)b);
}

int triangleNumber(int* nums, int numsSize) {
    qsort(nums, numsSize, sizeof(int), cmp);
    int ans = 0;
    for (int i = 0; i < numsSize; ++i) {
        int k = i;
        for (int j = i + 1; j < numsSize; ++j) {
            while (k + 1 < numsSize && nums[k + 1] < nums[i] + nums[j]) {
                ++k;
            }
            ans += fmax(k - j, 0);
        }
    }
    return ans;
}

9.27最大三角形面积

暴力枚举：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
double max(double a, double b) {
    return a > b ? a : b;
}

double Area(int x1, int y1, int x2, int y2, int x3, int y3) {
    return 0.5 * abs(x1 * y2 + x2 * y3 + x3 * y1 - x1 * y3 - x2 * y1 - x3 * y2);
}

double largestTriangleArea(int** points, int pointsSize, int* pointsColSize) {
    double ret = 0.0;
    for (int i = 0; i < pointsSize; i++) {
        for (int j = i + 1; j < pointsSize; j++) {
            for (int k = j + 1; k < pointsSize; k++) {
                double area = Area(points[i][0], points[i][1], points[j][0], points[j][1], points[k][0], points[k][1]);
                ret = max(ret, area);
            }
        }
    }
    return ret;   
}

9.28三角形的最大周长

题目：

1
给定由一些正数（代表长度）组成的数组 `nums` ，返回 *由其中三个长度组成的、**面积不为零**的三角形的最大周长* 。如果不能形成任何面积不为零的三角形，返回 `0`。

示例：

1
2
3
输入：nums = [2,1,2]
输出：5
解释：你可以用三个边长组成一个三角形:1 2 2。

答案：

简单的贪心

1
2
3
4
5
6
7
8
9
10
11
12
int cmp(const void *pa, const void *pb) {
    return *(int*)pa - *(int*)pb;
}
int largestPerimeter(int* nums, int numsSize) {
    qsort(nums, numsSize, sizeof(int), cmp);
    for (int i = numsSize - 1; i >= 2; --i) {
        if(nums[i - 2] + nums[i - 1] > nums[i]) {
            return nums[i - 2] + nums[i - 1] + nums[i];
        }
    }
    return 0;
}

9.29多边形三角形剖分的最低得分

题目:

1
2
3
4
5
你有一个凸的 `n` 边形，其每个顶点都有一个整数值。给定一个整数数组 `values` ，其中 `values[i]` 是第 `i` 个顶点的值（即 **顺时针顺序** ）。

假设将多边形 **剖分** 为 `n - 2` 个三角形。对于每个三角形，该三角形的值是顶点标记的**乘积**，三角剖分的分数是进行三角剖分后所有 `n - 2` 个三角形的值之和。

返回 *多边形进行三角剖分后可以得到的最低分* 。

示例 ：

img

1
2
3
输入：values = [1,2,3]
输出：6
解释：多边形已经三角化，唯一三角形的分数为 6。

题解：

区间dp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
// 记忆数组
unsigned int res_cache[51][51] = {0};

// res_cache表示以 start 和 end 为底边对其余所有点进行划分
unsigned int dp(int *A, int Asize, int start, int end)
{
    int i;
    int n = end - start;
    unsigned int res;
    unsigned int tmp;
    // 当n小于2的时候, 数组里面只有0-1,无法构成三角形
    if(n<2) return 0;

    if(res_cache[start][end]>0) return res_cache[start][end];

    if(n==2)
    {   // start = 0 end = 2

        res = A[start] * A[start+1] * A[end];

        res_cache[start][end] = res;
        return res;
    }
    res = -1;
    for(i=start+1; i<end; i++)
    {

        tmp = A[start] * A[i] * A[end];

        if(i == end-1)
        {
            tmp += dp(A, Asize, start, i);
        }
        else
        {
            tmp += dp(A, Asize, start, i) + dp(A, Asize, i ,end);
        }
        if(res > tmp)
        {
            res = tmp;
        }
    }  
    res_cache[start][end] = res;
    return res;
}



int minScoreTriangulation(int* A, int ASize)
{
    memset(res_cache, 0, sizeof(res_cache));
    return dp(A, ASize, 0, ASize-1);
}

9.30数组的三角和

标题:

1
2
3
4
5
6
7
8
9
给你一个下标从 0 开始的整数数组 nums ，其中 nums[i] 是 0 到 9 之间（两者都包含）的一个数字。

nums 的 三角和 是执行以下操作以后最后剩下元素的值：

1.nums 初始包含 n 个元素。如果 n == 1 ，终止 操作。否则，创建 一个新的下标从 0 开始的长度为 n - 1 的整数数组 newNums 。
2.对于满足 0 <= i < n - 1 的下标 i ，newNums[i] 赋值 为 (nums[i] + nums[i+1]) % 10 ，% 表示取余运算。
3.将 newNums 替换 数组 nums 。
4.从步骤 1 开始 重复 整个过程。
请你返回 nums 的三角和。

示例:

img

1
2
3
4
输入：nums = [1,2,3,4,5]
输出：8
解释：
上图展示了得到数组三角和的过程。

答案：

组合数，

1
2
3
4
5
6
7
8
9
10
class Solution:
    def triangularSum(self, nums: List[int]) -> int:
        n = len(nums)
        combination = 1
        ans = 0
        for i in range(n):
            ans = (ans + nums[i] * combination) % 10
            combination = combination *(n-i-1) // (i+1)
        return ans

10.1换水问题

题目:

1
2
3
4
5
超市正在促销，你可以用 numExchange 个空水瓶从超市兑换一瓶水。最开始，你一共购入了 numBottles 瓶水。

如果喝掉了水瓶中的水，那么水瓶就会变成空的。

给你两个整数 numBottles 和 numExchange ，返回你 最多 可以喝到多少瓶水。

示例:

1
2
3
4
5

输入：numBottles = 9, numExchange = 3
输出：13
解释：你可以用 3 个空瓶兑换 1 瓶水。
所以最多能喝到 9 + 3 + 1 = 13 瓶水。

题解：

简单的递归：

1
2
3
4
5
6
7
8
9
10
int change(int bottlenums, int changenums,int drinknums) {
    if(bottlenums / changenums > 0) {
        return change(bottlenums / changenums + bottlenums % changenums, changenums, drinknums + (bottlenums / changenums));
    }else {
        return drinknums;
    }
}
int numWaterBottles(int numBottles, int numExchange) {
    return change(numBottles, numExchange, numBottles);
}

10.2换水问题二

题目：

1
2
3
4
5
6
7
8
9
给你两个整数 numBottles 和 numExchange 。

numBottles 代表你最初拥有的满水瓶数量。在一次操作中，你可以执行以下操作之一：

喝掉任意数量的满水瓶，使它们变成空水瓶。
用 numExchange 个空水瓶交换一个满水瓶。然后，将 numExchange 的值增加 1 。
注意，你不能使用相同的 numExchange 值交换多批空水瓶。例如，如果 numBottles == 3 并且 numExchange == 1 ，则不能用 3 个空水瓶交换成 3 个满水瓶。

返回你 最多 可以喝到多少瓶水。

示例：

img

1
2
3
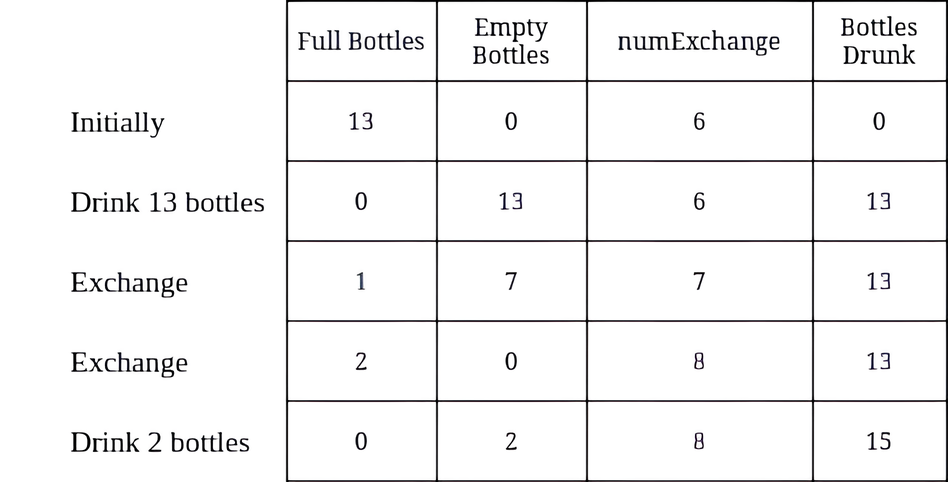
输入：numBottles = 13, numExchange = 6
输出：15
解释：上表显示了满水瓶的数量、空水瓶的数量、numExchange 的值，以及累计喝掉的水瓶数量。

题解:

数学解方程

1
2
3
4
5
6
7
8
int maxBottlesDrunk(int numBottles, int numExchange) {
    int a = 1;
    int b = 2 * numExchange -3;
    int c = -2 * numBottles;
    double delta = (double)b * b - 4.0 * a *c;
    int t = (int)ceil((-b + sqrt(delta)) / (2.0 * a));
    return numBottles + t - 1;
}