9.25三角形最小路径和

题目：

1
2
3
给定一个三角形 triangle ，找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

示例:

1
2
3
4
5
6
7
8
输入：triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出：11
解释：如下面简图所示：
   2
  3 4
 6 5 7
4 1 8 3
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

答案：

解法一：自上而下动态规划带备忘录：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int minimumTotal(int** triangle, int triangleSize, int* triangleColSize) {
    int f[triangleSize][triangleSize];
    memset(f,0,sizeof(f));
    f[0][0] = triangle[0][0];
    for (int i = 1; i < triangleSize; ++i) {
        f[i][0] = f[i - 1][0] + triangle[i][0];
        for(int j = 1; j < i; ++j) {
            f[i][j] = fmin(f[i - 1][j - 1],f[i - 1][j]) + triangle[i][j];
        }
        f[i][i] = f[i - 1][i - 1] + triangle[i][i];
    }
    int ret = f[triangleSize - 1][0];
    for(int i = 1; i < triangleSize; i++)
        ret = fmin(ret,f[triangleSize - 1][i]);
    return ret;
}

解法二:根据奇偶划分优化存储：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int minimumTotal(int** triangle, int triangleSize, int* triangleColSize) {
    int f[2][triangleSize];
    memset(f, 0, sizeof(f));
    f[0][0] = triangle[0][0];
    for (int i = 1; i < triangleSize; ++i) {
        int curr = i % 2;
        int prev = 1 - curr;
        f[curr][0] = f[prev][0] + triangle[i][0];
        for (int j = 1; j < i; ++j) {
            f[curr][j] = fmin(f[prev][j - 1], f[prev][j]) + triangle[i][j];
        }
        f[curr][i] = f[prev][i - 1] + triangle[i][i];
    }
    int ret = f[(triangleSize - 1) % 2][0];
    for (int i = 1; i < triangleSize; i++)
        ret = fmin(ret, f[(triangleSize - 1) % 2][i]);
    return ret;
}

9.26有效三角形个数

题目：

1
给定一个包含非负整数的数组 nums ，返回其中可以组成三角形三条边的三元组个数。

示例:

1
2
3
4
5
6
输入: nums = [2,2,3,4]
输出: 3
解释:有效的组合是: 
2,3,4 (使用第一个 2)
2,3,4 (使用第二个 2)
2,2,3

答案：

解法一，排序+二分查找:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int cmp(const void* a, const void* b) {
    return (*(int*)a - *(int*)b);
}
int triangleNumber(int* nums, int numsSize) {
    qsort(nums, numsSize,sizeof(int),*cmp);
    int ans = 0;
    for(int i = 0; i < numsSize; ++i) {
        for(int j = i + 1; j < numsSize; ++j) {
            int left = j + 1, right = numsSize - 1, k = j;
            while(left <= right) {
                int mid = (left + right) / 2;
                if(nums[mid] < nums[i] + nums[j]) {
                    k = mid;
                    left = mid + 1;
                }else {
                    right = mid - 1;
                }
            }
            ans += k-j;
        }
    }
    return ans;
}

优化后，解法二：双指针:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int cmp(const void* a, const void* b) {
    return (*(int*)a - *(int*)b);
}

int triangleNumber(int* nums, int numsSize) {
    qsort(nums, numsSize, sizeof(int), cmp);
    int ans = 0;
    for (int i = 0; i < numsSize; ++i) {
        int k = i;
        for (int j = i + 1; j < numsSize; ++j) {
            while (k + 1 < numsSize && nums[k + 1] < nums[i] + nums[j]) {
                ++k;
            }
            ans += fmax(k - j, 0);
        }
    }
    return ans;
}

9.27最大三角形面积

暴力枚举：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
double max(double a, double b) {
    return a > b ? a : b;
}

double Area(int x1, int y1, int x2, int y2, int x3, int y3) {
    return 0.5 * abs(x1 * y2 + x2 * y3 + x3 * y1 - x1 * y3 - x2 * y1 - x3 * y2);
}

double largestTriangleArea(int** points, int pointsSize, int* pointsColSize) {
    double ret = 0.0;
    for (int i = 0; i < pointsSize; i++) {
        for (int j = i + 1; j < pointsSize; j++) {
            for (int k = j + 1; k < pointsSize; k++) {
                double area = Area(points[i][0], points[i][1], points[j][0], points[j][1], points[k][0], points[k][1]);
                ret = max(ret, area);
            }
        }
    }
    return ret;   
}

9.28三角形的最大周长

题目：

1
给定由一些正数（代表长度）组成的数组 `nums` ，返回 *由其中三个长度组成的、**面积不为零**的三角形的最大周长* 。如果不能形成任何面积不为零的三角形，返回 `0`。

示例：

1
2
3
输入：nums = [2,1,2]
输出：5
解释：你可以用三个边长组成一个三角形:1 2 2。

答案：

简单的贪心

1
2
3
4
5
6
7
8
9
10
11
12
int cmp(const void *pa, const void *pb) {
    return *(int*)pa - *(int*)pb;
}
int largestPerimeter(int* nums, int numsSize) {
    qsort(nums, numsSize, sizeof(int), cmp);
    for (int i = numsSize - 1; i >= 2; --i) {
        if(nums[i - 2] + nums[i - 1] > nums[i]) {
            return nums[i - 2] + nums[i - 1] + nums[i];
        }
    }
    return 0;
}

9.29多边形三角形剖分的最低得分

题目:

1
2
3
4
5
你有一个凸的 `n` 边形，其每个顶点都有一个整数值。给定一个整数数组 `values` ，其中 `values[i]` 是第 `i` 个顶点的值（即 **顺时针顺序** ）。

假设将多边形 **剖分** 为 `n - 2` 个三角形。对于每个三角形，该三角形的值是顶点标记的**乘积**，三角剖分的分数是进行三角剖分后所有 `n - 2` 个三角形的值之和。

返回 *多边形进行三角剖分后可以得到的最低分* 。

示例 ：

img

1
2
3
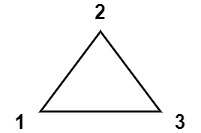
输入：values = [1,2,3]
输出：6
解释：多边形已经三角化，唯一三角形的分数为 6。

题解：

区间dp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
// 记忆数组
unsigned int res_cache[51][51] = {0};

// res_cache表示以 start 和 end 为底边对其余所有点进行划分
unsigned int dp(int *A, int Asize, int start, int end)
{
    int i;
    int n = end - start;
    unsigned int res;
    unsigned int tmp;
    // 当n小于2的时候, 数组里面只有0-1,无法构成三角形
    if(n<2) return 0;

    if(res_cache[start][end]>0) return res_cache[start][end];

    if(n==2)
    {   // start = 0 end = 2

        res = A[start] * A[start+1] * A[end];

        res_cache[start][end] = res;
        return res;
    }
    res = -1;
    for(i=start+1; i<end; i++)
    {

        tmp = A[start] * A[i] * A[end];

        if(i == end-1)
        {
            tmp += dp(A, Asize, start, i);
        }
        else
        {
            tmp += dp(A, Asize, start, i) + dp(A, Asize, i ,end);
        }
        if(res > tmp)
        {
            res = tmp;
        }
    }  
    res_cache[start][end] = res;
    return res;
}



int minScoreTriangulation(int* A, int ASize)
{
    memset(res_cache, 0, sizeof(res_cache));
    return dp(A, ASize, 0, ASize-1);
}

9.30数组的三角和

标题:

1
2
3
4
5
6
7
8
9
给你一个下标从 0 开始的整数数组 nums ，其中 nums[i] 是 0 到 9 之间（两者都包含）的一个数字。

nums 的 三角和 是执行以下操作以后最后剩下元素的值：

1.nums 初始包含 n 个元素。如果 n == 1 ，终止 操作。否则，创建 一个新的下标从 0 开始的长度为 n - 1 的整数数组 newNums 。
2.对于满足 0 <= i < n - 1 的下标 i ，newNums[i] 赋值 为 (nums[i] + nums[i+1]) % 10 ，% 表示取余运算。
3.将 newNums 替换 数组 nums 。
4.从步骤 1 开始 重复 整个过程。
请你返回 nums 的三角和。

示例:

img

1
2
3
4
输入：nums = [1,2,3,4,5]
输出：8
解释：
上图展示了得到数组三角和的过程。

答案：

组合数，

1
2
3
4
5
6
7
8
9
10
class Solution:
    def triangularSum(self, nums: List[int]) -> int:
        n = len(nums)
        combination = 1
        ans = 0
        for i in range(n):
            ans = (ans + nums[i] * combination) % 10
            combination = combination *(n-i-1) // (i+1)
        return ans

10.1换水问题

题目:

1
2
3
4
5
超市正在促销，你可以用 numExchange 个空水瓶从超市兑换一瓶水。最开始，你一共购入了 numBottles 瓶水。

如果喝掉了水瓶中的水，那么水瓶就会变成空的。

给你两个整数 numBottles 和 numExchange ，返回你 最多 可以喝到多少瓶水。

示例:

1
2
3
4
5

输入：numBottles = 9, numExchange = 3
输出：13
解释：你可以用 3 个空瓶兑换 1 瓶水。
所以最多能喝到 9 + 3 + 1 = 13 瓶水。

题解：

简单的递归：

1
2
3
4
5
6
7
8
9
10
int change(int bottlenums, int changenums,int drinknums) {
    if(bottlenums / changenums > 0) {
        return change(bottlenums / changenums + bottlenums % changenums, changenums, drinknums + (bottlenums / changenums));
    }else {
        return drinknums;
    }
}
int numWaterBottles(int numBottles, int numExchange) {
    return change(numBottles, numExchange, numBottles);
}

10.2换水问题二

题目：

1
2
3
4
5
6
7
8
9
给你两个整数 numBottles 和 numExchange 。

numBottles 代表你最初拥有的满水瓶数量。在一次操作中，你可以执行以下操作之一：

喝掉任意数量的满水瓶，使它们变成空水瓶。
用 numExchange 个空水瓶交换一个满水瓶。然后，将 numExchange 的值增加 1 。
注意，你不能使用相同的 numExchange 值交换多批空水瓶。例如，如果 numBottles == 3 并且 numExchange == 1 ，则不能用 3 个空水瓶交换成 3 个满水瓶。

返回你 最多 可以喝到多少瓶水。

示例：

img

1
2
3
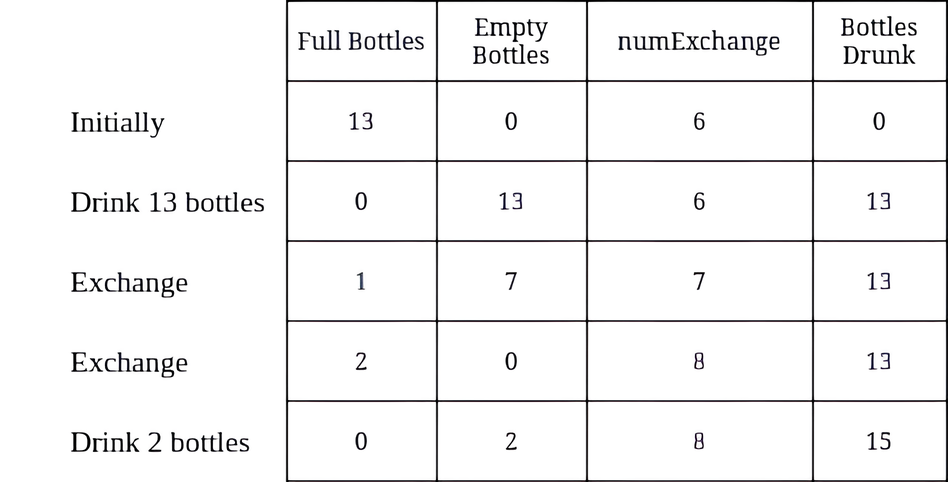
输入：numBottles = 13, numExchange = 6
输出：15
解释：上表显示了满水瓶的数量、空水瓶的数量、numExchange 的值，以及累计喝掉的水瓶数量。

题解:

数学解方程

1
2
3
4
5
6
7
8
int maxBottlesDrunk(int numBottles, int numExchange) {
    int a = 1;
    int b = 2 * numExchange -3;
    int c = -2 * numBottles;
    double delta = (double)b * b - 4.0 * a *c;
    int t = (int)ceil((-b + sqrt(delta)) / (2.0 * a));
    return numBottles + t - 1;
}

10.3接雨水二

题目：

1
给你一个 m x n 的矩阵，其中的值均为非负整数，代表二维高度图每个单元的高度，请计算图中形状最多能接多少体积的雨水。

示例:

img

1
2
3
输入: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
输出: 4
解释: 下雨后，雨水将会被上图蓝色的方块中。总的接雨水量为1+2+1=4。

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <limits.h>

// 定义方向数组：上、右、下、左
int dirs[4][2] = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};

// 最小堆节点结构
typedef struct {
    int i, j, height;
} Cell;

// 最小堆结构
typedef struct {
    Cell* data;
    int size;
    int capacity;
} MinHeap;

// 创建最小堆
MinHeap* createMinHeap(int capacity) {
    MinHeap* heap = (MinHeap*)malloc(sizeof(MinHeap));
    heap->data = (Cell*)malloc(sizeof(Cell) * capacity);
    heap->size = 0;
    heap->capacity = capacity;
    return heap;
}

// 交换两个节点
void swap(Cell* a, Cell* b) {
    Cell temp = *a;
    *a = *b;
    *b = temp;
}

// 上浮操作
void heapifyUp(MinHeap* heap, int idx) {
    while (idx > 0) {
        int parent = (idx - 1) / 2;
        if (heap->data[parent].height <= heap->data[idx].height) {
            break;
        }
        swap(&heap->data[parent], &heap->data[idx]);
        idx = parent;
    }
}

// 下沉操作
void heapifyDown(MinHeap* heap, int idx) {
    int left, right, smallest;
    int size = heap->size;
    
    while (idx < size) {
        left = 2 * idx + 1;
        right = 2 * idx + 2;
        smallest = idx;
        
        if (left < size && heap->data[left].height < heap->data[smallest].height) {
            smallest = left;
        }
        if (right < size && heap->data[right].height < heap->data[smallest].height) {
            smallest = right;
        }
        
        if (smallest == idx) break;
        
        swap(&heap->data[idx], &heap->data[smallest]);
        idx = smallest;
    }
}

// 插入节点
void push(MinHeap* heap, Cell cell) {
    if (heap->size >= heap->capacity) return;
    
    heap->data[heap->size] = cell;
    heapifyUp(heap, heap->size);
    heap->size++;
}

// 弹出最小节点
Cell pop(MinHeap* heap) {
    if (heap->size == 0) {
        Cell empty = {-1, -1, -1};
        return empty;
    }
    
    Cell minCell = heap->data[0];
    heap->data[0] = heap->data[heap->size - 1];
    heap->size--;
    heapifyDown(heap, 0);
    
    return minCell;
}

// 检查坐标是否在矩阵范围内
bool isValid(int i, int j, int m, int n) {
    return i >= 0 && i < m && j >= 0 && j < n;
}

int trapRainWater(int** heightMap, int heightMapSize, int* heightMapColSize) {
    if (heightMapSize < 3 || heightMapColSize[0] < 3) return 0;
    
    int m = heightMapSize;
    int n = heightMapColSize[0];
    int totalWater = 0;
    
    // 创建访问标记数组
    bool** visited = (bool**)malloc(sizeof(bool*) * m);
    for (int i = 0; i < m; i++) {
        visited[i] = (bool*)calloc(n, sizeof(bool));
    }
    
    // 创建最小堆
    MinHeap* heap = createMinHeap(m * n);
    
    // 将边界的所有单元格加入堆中
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {
                push(heap, (Cell){i, j, heightMap[i][j]});
                visited[i][j] = true;
            }
        }
    }
    
    // 处理堆中的单元格
    while (heap->size > 0) {
        Cell current = pop(heap);
        int currentI = current.i;
        int currentJ = current.j;
        int currentHeight = current.height;
        
        // 检查四个方向
        for (int k = 0; k < 4; k++) {
            int ni = currentI + dirs[k][0];
            int nj = currentJ + dirs[k][1];
            
            if (isValid(ni, nj, m, n) && !visited[ni][nj]) {
                // 如果相邻单元格的高度小于当前边界高度，可以积水
                if (heightMap[ni][nj] < currentHeight) {
                    totalWater += currentHeight - heightMap[ni][nj];
                }
                
                // 将相邻单元格加入堆中，高度取较大值
                int newHeight = heightMap[ni][nj] > currentHeight ? 
                               heightMap[ni][nj] : currentHeight;
                push(heap, (Cell){ni, nj, newHeight});
                visited[ni][nj] = true;
            }
        }
    }
    
    // 释放内存
    for (int i = 0; i < m; i++) {
        free(visited[i]);
    }
    free(visited);
    free(heap->data);
    free(heap);
    
    return totalWater;
}

10.4盛最多水的容器

题目：

1
2
3
4
5
6
7
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例:

img

1
2
3
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

题解：

双指针：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int max(int a, int b) {
    if(a > b) return a;
    return b;
}

int min(int a, int b) {
    if(a > b) return b;
    return a;
}

int maxArea(int* height, int heightSize) {
    int i = 0;
    int j = heightSize - 1;
    int result = 0;
    while(i < j) {
        int area = (j - i) * min(height[i], height[j]);
        result = max(result, area);
        if(height[i] < height[j]) {
            i++;
        }else {
            j--;
        }
    }
    return result;
}

10.5太平洋大西洋水流问题

题目：

1
2
3
4
5
6
7
有一个 m × n 的矩形岛屿，与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界，而 “大西洋” 处于大陆的右边界和下边界。

这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights ， heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。

岛上雨水较多，如果相邻单元格的高度 小于或等于 当前单元格的高度，雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。

返回网格坐标 result 的 2D 列表 ，其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。

示例：

img

1
2
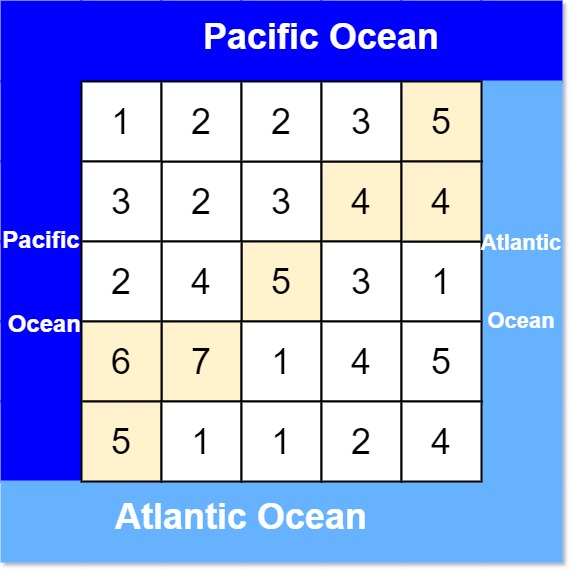
输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

题解：

dfs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
 static const int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
 
 void dfs(int row, int col, bool ** ocean, int ** heights, int m, int n) {
    if (ocean[row][col]) {
        return;
    }
    ocean[row][col] = true;
    for (int i = 0; i < 4; i++) {
        int newRow = row + dirs[i][0], newCol = col + dirs[i][1];
        if (newRow >= 0 && newRow < m && newCol >= 0 && newCol < n && heights[newRow][newCol] >= heights[row][col]) {
            dfs(newRow, newCol, ocean, heights, m, n);
        }
    }
}


int** pacificAtlantic(int** heights, int heightsSize, int* heightsColSize, int* returnSize, int** returnColumnSizes) {
    int m = heightsSize;
    int n = heightsColSize[0];
        bool ** pacific = (bool **)malloc(sizeof(bool *) * m);
        bool ** atlantic = (bool **)malloc(sizeof(bool *) * m);
        for (int i = 0; i < m; i++) {
            pacific[i] = (bool *)malloc(sizeof(bool) * n);
            atlantic[i] = (bool *)malloc(sizeof(bool) * n);
            memset(pacific[i], 0, sizeof(bool) * n);
            memset(atlantic[i], 0, sizeof(bool) * n);
        }

        for (int i = 0; i < m; i++) {
            dfs(i, 0, pacific, heights, m, n);
        }
        for (int j = 1; j < n; j++) {
            dfs(0, j, pacific, heights, m, n);
        }
        for (int i = 0; i < m; i++) {
            dfs(i, n - 1, atlantic, heights, m, n);
        }
        for (int j = 0; j < n - 1; j++) {
            dfs(m - 1, j, atlantic, heights, m, n);
        }
        int ** result = (int **)malloc(sizeof(int *) * m * n);
        *returnColumnSizes = (int *)malloc(sizeof(int) * m * n);
        int pos = 0;
        for (int i = 0; i < m * n; i++) {
            result[i] = (int *)malloc(sizeof(int) * 2);
            (*returnColumnSizes)[i] = 2;
        }
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (pacific[i][j] && atlantic[i][j]) {
                    result[pos][0] = i;
                    result[pos][1] = j;
                    pos++;
                }
            }
            free(pacific[i]);
            free(atlantic[i]);
        }
        free(pacific);
        free(atlantic);
        *returnSize = pos;
        return result;

}

10.6水位上升的游泳池游泳

题目：

1
2
3
4
5
在一个 `n x n` 的整数矩阵 `grid` 中，每一个方格的值 `grid[i][j]` 表示位置 `(i, j)` 的平台高度。

当开始下雨时，在时间为 `t` 时，水池中的水位为 `t` 。你可以从一个平台游向四周相邻的任意一个平台，但是前提是此时水位必须同时淹没这两个平台。假定你可以瞬间移动无限距离，也就是默认在方格内部游动是不耗时的。当然，在你游泳的时候你必须待在坐标方格里面。

你从坐标方格的左上平台 `(0，0)` 出发。返回 *你到达坐标方格的右下平台 `(n-1, n-1)` 所需的最少时间 。*

示例：

img

1
2
3
4
5
6
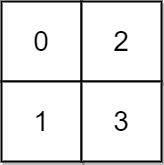
输入: grid = [[0,2],[1,3]]
输出: 3
解释:
时间为0时，你位于坐标方格的位置为 (0, 0)。
此时你不能游向任意方向，因为四个相邻方向平台的高度都大于当前时间为 0 时的水位。
等时间到达 3 时，你才可以游向平台 (1, 1). 因为此时的水位是 3，坐标方格中的平台没有比水位 3 更高的，所以你可以游向坐标方格中的任意位置

题解:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
int directions[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};

bool check(int** grid, int gridSize, int threshold) {
    if (grid[0][0] > threshold) {
        return false;
    }
    int visited[gridSize][gridSize];
    memset(visited, 0, sizeof(visited));
    visited[0][0] = 1;
    int q[gridSize * gridSize][2];
    int left = 0, right = 0;
    q[right][0] = 0, q[right++][1] = 0;

    while (left < right) {
        int i = q[left][0], j = q[left++][1];

        for (int k = 0; k < 4; k++) {
            int ni = i + directions[k][0], nj = j + directions[k][1];
            if (ni >= 0 && ni < gridSize && nj >= 0 && nj < gridSize) {
                if (visited[ni][nj] == 0 && grid[ni][nj] <= threshold) {
                    q[right][0] = ni, q[right++][1] = nj;
                    visited[ni][nj] = 1;
                }
            }
        }
    }
    return visited[gridSize - 1][gridSize - 1] == 1;
}

int swimInWater(int** grid, int gridSize, int* gridColSize) {
    int left = 0, right = gridSize * gridSize - 1;
    while (left < right) {
        int mid = (left + right) >> 1;
        if (check(grid, gridSize, mid)) {
            right = mid;
        } else {
            left = mid + 1;
        }
    }
    return left;
}

10.14检测相邻递增子数组一

题目:

1
2
3
4
5
6
7
8
给你一个由 `n` 个整数组成的数组 `nums` 和一个整数 `k`，请你确定是否存在 **两个** **相邻** 且长度为 `k` 的 **严格递增** 子数组。具体来说，需要检查是否存在从下标 `a` 和 `b` (`a < b`) 开始的 **两个** 子数组，并满足下述全部条件：

- 这两个子数组 `nums[a..a + k - 1]` 和 `nums[b..b + k - 1]` 都是 **严格递增** 的。
- 这两个子数组必须是 **相邻的**，即 `b = a + k`。

如果可以找到这样的 **两个** 子数组，请返回 `true`；否则返回 `false`。

**子数组** 是数组中的一个连续 **非空** 的元素序列。

示例:

1
2
3
4
5
6
7
8
9
**输入：**nums = [2,5,7,8,9,2,3,4,3,1], k = 3

**输出：**true

**解释：**

- 从下标 `2` 开始的子数组为 `[7, 8, 9]`，它是严格递增的。
- 从下标 `5` 开始的子数组为 `[2, 3, 4]`，它也是严格递增的。
- 两个子数组是相邻的，因此结果为 `true`。

题解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
int max(int a, int b) {
    if(a > b) return a;
    return b;
}

int min(int a, int b) {
    if(a > b) return b;
    return a;
}

bool hasIncreasingSubarrays(int* nums, int numsSize, int k) {
    int cur = 1;
    int pre = 0;
    int amount = 0;
    for(int i =0; i < numsSize - 1; i++) {
        if(nums[i + 1] > nums[i]) {
            cur++;
        }else{
            pre = cur;
            cur = 1;
        }
        amount = max(amount, min(pre, cur));
        amount = max(amount, cur / 2);
    }
    return amount >= k;
}

10.17执行操作后的最大分割数量

题目：

1
2
3
4
5
6
7
8
9
给你一个下标从 0 开始的字符串 s 和一个整数 k。

你需要执行以下分割操作，直到字符串 s 变为 空：

选择 s 的最长 前缀，该前缀最多包含 k 个 不同 字符。
删除 这个前缀，并将分割数量加一。如果有剩余字符，它们在 s 中保持原来的顺序。
执行操作之 前 ，你可以将 s 中 至多一处 下标的对应字符更改为另一个小写英文字母。

在最优选择情形下改变至多一处下标对应字符后，用整数表示并返回操作结束时得到的 最大 分割数量。

示例:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
输入：s = "accca", k = 2

输出：3

解释：

最好的方式是把 s[2] 变为除了 a 和 c 之外的东西，比如 b。然后它变成了 "acbca"。

然后我们执行以下操作：

最多包含 2 个不同字符的最长前缀是 "ac"，我们删除它然后 s 变为 "bca"。
现在最多包含 2 个不同字符的最长前缀是 "bc"，所以我们删除它然后 s 变为 "a"。
最后，我们删除 "a" 并且 s 变成空串，所以该过程结束。
进行操作时，字符串被分成 3 个部分，所以答案是 3。

题解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
#include <stdio.h>
#include <string.h>
#include <stdlib.h>

int cal(char *s, int len, int k) {
    if (len == 0) return 0;
    
    int freq[26] = {0};
    int distinct = 0;
    int partitions = 0;
    int start = 0;
    
    while (start < len) {
        memset(freq, 0, sizeof(freq));
        distinct = 0;
        int i = start;
        while (i < len) {
            int idx = s[i] - 'a';
            if (freq[idx] == 0) {
                if (distinct == k) break;
                distinct++;
            }
            freq[idx]++;
            i++;
        }
        partitions++;
        start = i;
    }
    
    return partitions;
}

int maxPartitionsAfterOperations(char* s, int k) {
    int totalLen = strlen(s);
    
    // 特殊情况：k=26
    if (k == 26) return 1;
    
    // 预处理后缀信息
    int* sufSeg = (int*)malloc(totalLen * sizeof(int));
    int* sufMask = (int*)malloc(totalLen * sizeof(int));
    
    // 从右到左计算后缀信息
    sufSeg[totalLen-1] = 1;
    sufMask[totalLen-1] = 1 << (s[totalLen-1] - 'a');
    
    for (int i = totalLen-2; i >= 0; i--) {
        int charBit = 1 << (s[i] - 'a');
        int currentMask = sufMask[i+1];
        int currentSize = 0;
        
        // 计算当前mask的大小
        for (int j = 0; j < 26; j++) {
            if (currentMask & (1 << j)) currentSize++;
        }
        
        if ((currentMask & charBit) || currentSize < k) {
            // 可以加入当前段
            sufSeg[i] = sufSeg[i+1];
            sufMask[i] = currentMask | charBit;
        } else {
            // 需要新开一段
            sufSeg[i] = sufSeg[i+1] + 1;
            sufMask[i] = charBit;
        }
    }
    
    int result = sufSeg[0]; // 不修改任何字符的情况
    int preSeg = 0;
    int preMask = 0;
    
    for (int i = 0; i < totalLen; i++) {
        // 计算前缀信息（到i-1位置）
        if (i > 0) {
            int charBit = 1 << (s[i-1] - 'a');
            int preSize = 0;
            
            // 计算preMask的大小
            for (int j = 0; j < 26; j++) {
                if (preMask & (1 << j)) preSize++;
            }
            
            if ((preMask & charBit) || preSize < k) {
                preMask |= charBit;
            } else {
                preSeg++;
                preMask = charBit;
            }
        }
        
        // 获取后缀信息（从i+1位置开始）
        int suf_seg = (i == totalLen-1) ? 0 : sufSeg[i+1];
        int suf_mask = (i == totalLen-1) ? 0 : sufMask[i+1];
        
        // 计算并集大小
        int unionMask = preMask | suf_mask;
        int unionSize = 0;
        int preSize = 0;
        int sufSize = 0;
        
        for (int j = 0; j < 26; j++) {
            if (preMask & (1 << j)) preSize++;
            if (suf_mask & (1 << j)) sufSize++;
            if (unionMask & (1 << j)) unionSize++;
        }
        
        int tmp;
        // 分类讨论
        if (unionSize < k) {
            // 情况1：必须合并成一段
            tmp = 1;
        } else if (unionSize < 26 && preSize == k && sufSize == k) {
            // 情况2：可以多分一段
            tmp = preSeg + suf_seg + 2;
        } else {
            // 情况3：总段数不变
            tmp = preSeg + suf_seg + 1;
        }
        
        result = result > tmp ? result : tmp;
    }
    
    free(sufSeg);
    free(sufMask);
    return result;
}

10.18执行操作后不同元素的最大数量

题目：

1
2
3
4
5
6
给你一个整数数组 nums 和一个整数 k。

你可以对数组中的每个元素 最多 执行 一次 以下操作：

将一个在范围 [-k, k] 内的整数加到该元素上。
返回执行这些操作后，nums 中可能拥有的不同元素的 最大 数量。

示例 :

1
2
3
4
5
6
7
**输入**：nums = [1,2,2,3,3,4], k = 2

**输出**：6

**解释**：

对前四个元素执行操作，`nums` 变为 `[-1, 0, 1, 2, 3, 4]`，可以获得 6 个不同的元素。

题解:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int compare(const void* a, const void* b) {
    return (*(int*)a - *(int*)b);
}

int maxDistinctElements(int* nums, int numsSize, int k) {
    qsort(nums, numsSize, sizeof(int), compare);
    int cnt = 0;
    int prev = INT_MIN;
    
    for (int i = 0; i < numsSize; i++) {
        int num = nums[i];
        int curr = fmin(fmax(num - k, prev + 1), num + k);
        if (curr > prev) {
            cnt++;
            prev = curr;
        }
    }
    return cnt;
}

10.19

题目：

1
2
3
4
5
6
7
8
9
给你一个字符串 s 以及两个整数 a 和 b 。其中，字符串 s 的长度为偶数，且仅由数字 0 到 9 组成。

你可以在 s 上按任意顺序多次执行下面两个操作之一：

累加：将  a 加到 s 中所有下标为奇数的元素上（下标从 0 开始）。数字一旦超过 9 就会变成 0，如此循环往复。例如，s = "3456" 且 a = 5，则执行此操作后 s 变成 "3951"。
轮转：将 s 向右轮转 b 位。例如，s = "3456" 且 b = 1，则执行此操作后 s 变成 "6345"。
请你返回在 s 上执行上述操作任意次后可以得到的 字典序最小 的字符串。

如果两个字符串长度相同，那么字符串 a 字典序比字符串 b 小可以这样定义：在 a 和 b 出现不同的第一个位置上，字符串 a 中的字符出现在字母表中的时间早于 b 中的对应字符。例如，"0158” 字典序比 "0190" 小，因为不同的第一个位置是在第三个字符，显然 '5' 出现在 '9' 之前。

示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
输入：s = "5525", a = 9, b = 2
输出："2050"
解释：执行操作如下：
初态："5525"
轮转："2555"
累加："2454"
累加："2353"
轮转："5323"
累加："5222"
累加："5121"
轮转："2151"
累加："2050"
无法获得字典序小于 "2050" 的字符串。

题解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
char * findLexSmallestString(char * s, int a, int b) {
    int n = strlen(s);
    int vis[n];
    memset(vis, 0, sizeof(vis));
    char *res = (char *)calloc(sizeof(char), n + 1);
    strcpy(res, s);
    // 将 s 延长一倍，方便截取轮转后的字符串 t
    char str[2 * n + 1];
    sprintf(str, "%s%s", s, s);
    for (int i = 0; vis[i] == 0; i = (i + b) % n) {
        vis[i] = 1;
        for (int j = 0; j < 10; j++) {
            int k_limit = b % 2 == 0 ? 0 : 9;
            for (int k = 0; k <= k_limit; k++) {
                // 每次进行累加之前，重新截取 t
                char t[n + 1];
                strncpy(t, str + i, n);
                t[n] = '\0';
                for (int p = 1; p < n; p += 2) {
                    t[p] = '0' + (t[p] - '0' + j * a) % 10;
                }
                for (int p = 0; p < n; p += 2) {
                    t[p] = '0' + (t[p] - '0' + k * a) % 10;
                }
                if (strcmp(t, res) < 0) {
                    strcpy(res, t);
                }
            }
        }
    }
    return res;
}